8 Statistisch testen

8.1 t-Test

Der Begriff “t-Test” und “Student’s t-Test” werden oft synonym verwendet. Der t-Test ist aber nur einer von vielen Tests um zu bestimmen, ob es signifikante Unterschiede zwischen den Mittelwerten zweier Gruppen gibt.

8.1.1 Unterschiedliche Arten

Ein t-Test kann auf verschiedene Arten durchgeführt werden, je nach Situation und Vorannahmen:

Ein-Stichproben-t-Test: Testet, ob der Mittelwert einer Stichprobe von einem bekannten Mittelwert abweicht.
Unabhängiger t-Test / Zweistichproben-t-Test: Testet Unterschiede zwischen den Mittelwerten von zwei unabhängigen Gruppen.
Abhängiger t-Test / Paarweiser t-Test: Testet Unterschiede zwischen den Mittelwerten von verbundenen oder gepaarten Stichproben (z.B. Vorher-Nachher-Messungen).

8.1.2 Vorraussetzungen

Der einfache t-Test setzt die folgenden Charakteristika der Daten voraus:

Unabhängigkeit der Beobachtungen: Jede Versuchsperson sollte nur einer Gruppe angehören. Es sollte keine Beziehung zwischen den Beobachtungen in jeder Gruppe geben.
- Sollte diese Annahme nicht erfüllt sein, muss ein paarweiser t-Test verwendet werden.
Keine signifikanten Ausreißer in den beiden Gruppen: Ausreißer können das Testergebnis stark beeinflussen und sollten daher vermieden werden.
- Sollte diese Annahme nicht erfüllt sein, sollte man sich Gedanken machen, ob ein statistischer Test mit den Aussreißern Sinn ergibt. Eventuell ist eine Datenbereinigung sinnvoll oder die Verwendung von Teststatistiken die empfindlich gegenüber Ausreißern sind (z.B.: Mann-Whitney-U-Test).
Varianzgleichheit: Die Varianz der abhängigen Variable sollte in jeder Gruppe gleich sein. Zu beachten ist, dass der Welch-t-Test diese Annahme nicht voraussetzt.
- Sollte diese Annahme nicht erfüllt sein, ist der Welch-t-Tests eine Alternative, die zwar eine niedrigere statistische Power hat, aber die Annahme der Varianzgleichheit nicht benötigt.

Tipp

Wenn Sie einen Test durchführen wollen, stellen Sie sicher, dass Ihre Daten die oben genannten Voraussetzungen erfüllen.

8.1.3 Gepaarter t-Test

Ein gepaarter t-Test (paired t-test) wird durchgeführt, wenn man zwei Variablen verbundener Beobachtungen hat. Der gepaarte t-Test ist geeignet, wenn die Beobachtungen innerhalb jedes Paares korreliert (abhängig) sind und man überprüfen möchte, ob es einen statistisch signifikanten Unterschied in ihren Mittelwerten gibt. Typische Situationen sind:

Wiederholte Messungen: Die gleiche Gruppe von Subjekten oder Einheiten wird unter verschiedenen Bedingungen, Behandlungen oder Zeitpunkten gemessen. Beispiel: Vorher-Nachher-Messungen derselben Personen.
Gepaarte Paare: Beobachtungen sind auf irgendeine Weise natürlich gepaart, z.B. bei einem Cross-Over-Studien-Design, wo jedes Subjekt beide Behandlungen erhält und die Ergebnisse für jedes Subjekt verglichen werden.
Vorher-Nachher-Vergleiche: Messungen vor und nach einer Intervention oder einem Ereignis für dieselbe Gruppe von Subjekten.
Links-rechts-Vergleiche: Vergleich von Messungen von der linken und rechten Seite des Körpers oder von zwei eng verwandten Proben, wie Geschwistern oder Zwillingen.

8.1.4 t-Testen mit R

In R bietet die Funktion t.test mehrere Argumente, die angepasst werden können. Um die voreingestellten Werte der Argumente zu sehen, ist ein Blick in die Dokumentation notwendig. Hierzu einfach ?t.test in die R-Konsole eingeben. Im Folgenden gebe ich eine Übersicht über die wichtigsten Argumente und deren Standardwerte:

t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"),
       mu = 0,
       paired = FALSE,
       var.equal = FALSE,
       conf.level = 0.95)

Beschreibung der Argumente:

x: Ein numerischer Vektor der Datenwerte.
y: Ein optionaler numerischer Vektor der Datenwerte. Wenn y nicht NULL ist, wird ein Zweistichprobentest durchgeführt.
alternative: Gibt die Form der Alternativhypothese an. Kann sein:
- "two.sided" (zweiseitig) (Standard)
- "less" (einseitig, Test auf kleiner)
- "greater" (einseitig, Test auf größer)
mu: Der wahre Mittelwert oder die Differenz der Mittelwerte unter der Nullhypothese. Standard ist 0.
paired: Ein logischer Wert, der angibt, ob ein gepaarter Test durchgeführt wird. Standard ist FALSE.
var.equal: Ein logischer Wert, der angibt, ob die beiden Populationen gleiche Varianzen haben. Standard ist FALSE.
conf.level: Das Konfidenzniveau des Intervalls. Standard ist 0.95.

Tipp

Stellen Sie sicher, dass ihre Daten numerische Variablen sind. In dem Datensatz df_cleaned, den ich in Kapitel 3 beschreibe sind die Daten aber als Faktor Variablen kodiert. Dies kann einfach geändert werden:

if (!require(pacman)) install.packages("pacman")

Loading required package: pacman

pacman::p_load(tidyverse, janitor, psych, tinytable, ggstats, car, ggstatsplot,
               modelsummary, knitr, kableExtra, ggpubr, rstatix, rempsyc)
rm(list = ls())

load("~/Dropbox/hsf/github/ewa/ss_24/read_in_71/data_71.RData")

df_test <- df_cleaned |> 
  mutate_at(vars(starts_with("item_")), as.numeric)

head(df_test)

# A tibble: 6 × 31
     id group item_1 item_2 item_3 item_4 item_5 item_6 item_7 item_8 item_9
  <int> <int>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
1     1     1      4      3      4      5      2      3      2      2      3
2     2     0      4      4      3      4      4      5      3      3      4
3     3     1      1      3      4      3      3      4      4      3      4
4     4     1      3      3      5      3      2      3      1      3      2
5     5     1      3      3      2      5      4      4      4      3      4
6     6     0      3      3      2      2      2      3      2      2      2
# ℹ 20 more variables: item_10 <dbl>, item_11 <dbl>, item_12 <dbl>,
#   item_13 <dbl>, item_14 <dbl>, item_15 <dbl>, item_16 <dbl>, item_17 <dbl>,
#   item_18 <dbl>, item_19 <dbl>, item_20 <dbl>, item_21 <dbl>, outlier <dbl>,
#   has_outlier <lgl>, count_larger_5 <int>, count_typos <int>,
#   has_larger_5_notypos <lgl>, has_typos <lgl>, has_nas <lgl>, complete <lgl>

Long und Wide Format

Oft ist es empfehlenswert den Datensatz in das sogenannte Long Format zu überführen. Wie zwischen dem Long-Format und den Wide-Format gewechselt werden kann, bitte ich Wickham & Grolemund (2023): 5.3 Lengthening data zu entnehmen. Hier ein Beispiel:

df_test_long <- df_test |> 
  pivot_longer(cols = starts_with("item_"), # Zu pivotierende Spalten
               names_to = "item",           # Neue Spalte für die Namen der Items
               values_to = "value")  |>     # Neue Spalte für die Werte der Items
  select(id, group, complete, item, value)
head(df_test_long)

Wickham, H., & Grolemund, G. (2023). R for Data Science (2e). https://r4ds.hadley.nz/

8.2 Beispiel

Kopieren Sie dieses Skript und führen Sie es aus:

## ----echo=TRUE, message=FALSE-----------------------------------------------
if (!require(pacman)) install.packages("pacman")
pacman::p_load(tidyverse, janitor, psych, tinytable, ggstats, car, ggstatsplot, 
               modelsummary, knitr, kableExtra, ggpubr, rstatix, rempsyc)
rm(list = ls())

load("~/Dropbox/hsf/github/ewa/ss_24/read_in_71/data_71.RData")

# Zuerst wandle ich die Daten etwas um, so dass ich keine Faktorvariable mehr habe:
df_test <- df_cleaned |> 
  mutate_at(vars(starts_with("item_")), as.numeric)

# ##########################
# Ein-Stichproben t-Test
# ##########################

t.test(df_test$item_1, mu = 1)
t.test(df_test$item_1, mu = 3)

# Standardmäßig führt t.test einen zweiseitigen Test durch:
t.test(df_test$item_1, mu = 3, alternative = "two.sided")

# Sie können einen Test für einen Teil der Daten durchführen, indem Sie ein Argument der t.test-Funktion verwenden:
t.test(df_test$item_1, 
       mu = 3, 
       alternative = "two.sided",
       subset(df_test, group == 0))

t.test(df_test$item_1, 
       mu = 3,
       alternative = "greater")

t.test(df_test$item_1, 
       mu = 3,
       alternative = "less")

# ##########################
# Zweiseitiger t-Test in R
# ##########################

# ----------------------------
# Für Daten im Breitformat:
# ----------------------------

# Welch-Test
t.test(df_test$item_1, df_test$item_2, data = df_test)

# Student's t-Test
t.test(df_test$item_1, df_test$item_2, data = df_test, var.equal = TRUE)

# Welch-Test
t.test(df_test$item_1, df_test$item_2, data = df_test, 
       paired = TRUE, 
       var.equal = TRUE)

## Die Antworten kommen von der selben Person, daher paired = TRUE

# ----------------------------
# Für Daten im Langformat:
# ----------------------------

# Test, ob das item_1 in beiden Gruppen gleich ist

# Erstelle ein Boxplot von item_1 über Gruppen mit ggplot2
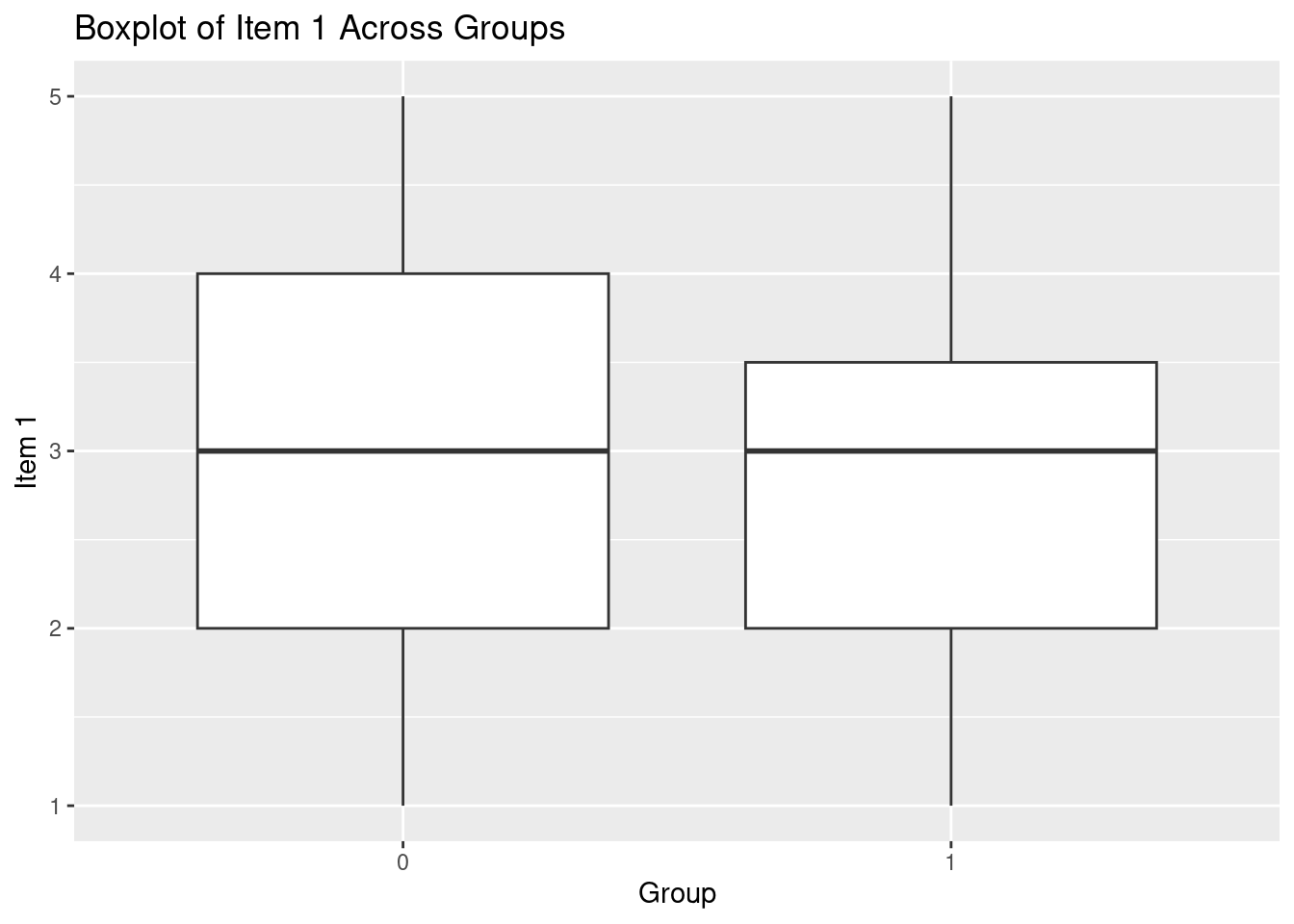
ggplot(df_test, aes(x = factor(group), y = item_1)) +
  geom_boxplot() +
  labs(x = "Group", y = "Item 1") +
  ggtitle("Boxplot of Item 1 Across Groups")

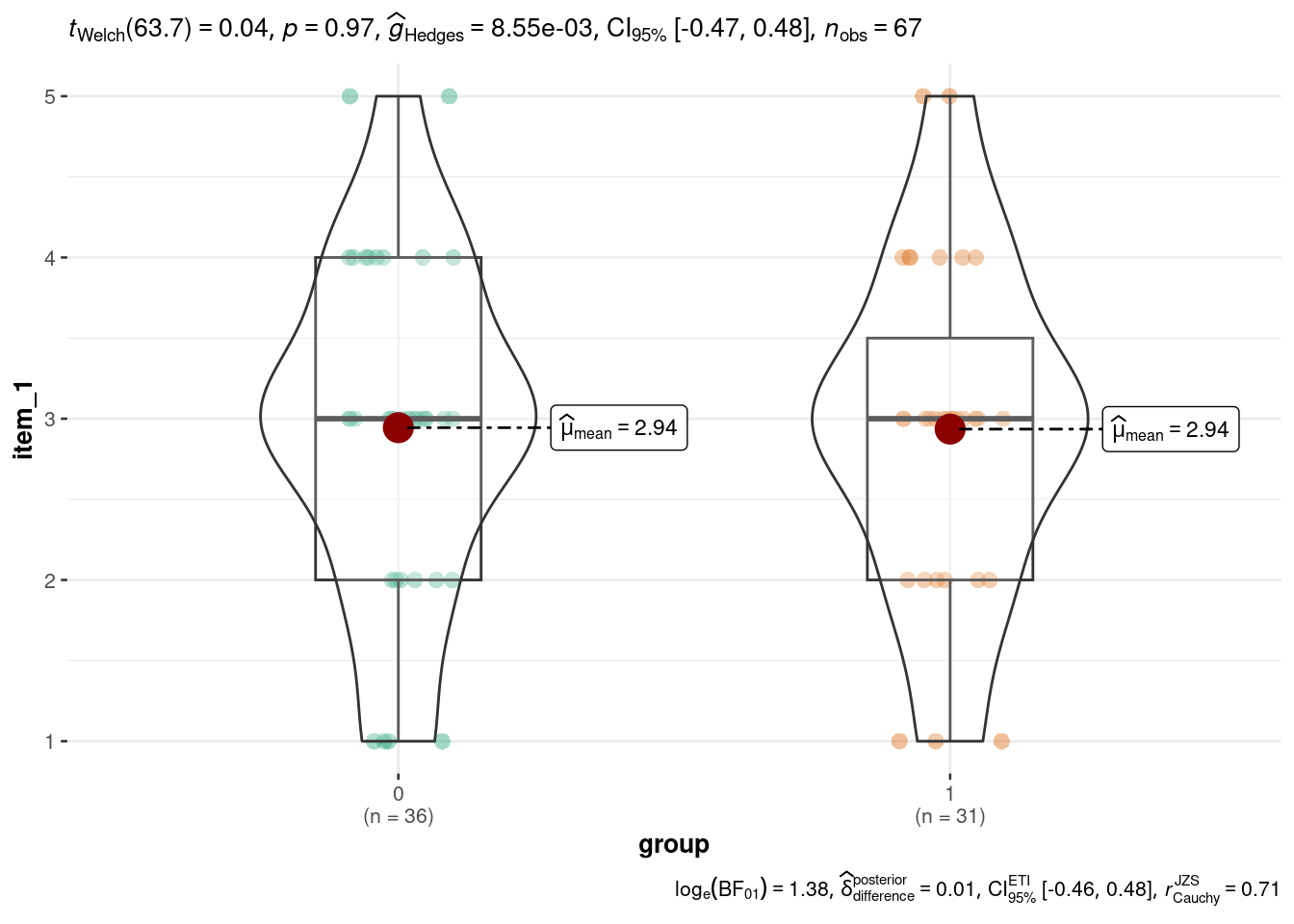
ggbetweenstats(
  data = df_test,
  x = group,
  y = item_1
)

## Wenn Normalitäts- und Varianzannahmen erfüllt sind:
t.test(item_1 ~ group, data = df_test, var.equal = FALSE)

# OK, aber wie testet man nun,
# ob die Antworten aller items in den jeweiligen Gruppen gleich sind? 

# Zuerst empfiehlt sich eine Umwandlung in das Langformat:
df_test_long <- df_test |> 
  pivot_longer(cols = starts_with("item_"), # Zu pivotierende Spalten
               names_to = "item",           # Neue Spalte für die Namen der Items
               values_to = "value")  |>     # Neue Spalte für die Werte der Items
  select(id, group, complete, item, value)

# Erstelle ein Boxplot von value über Gruppen mit ggplot2
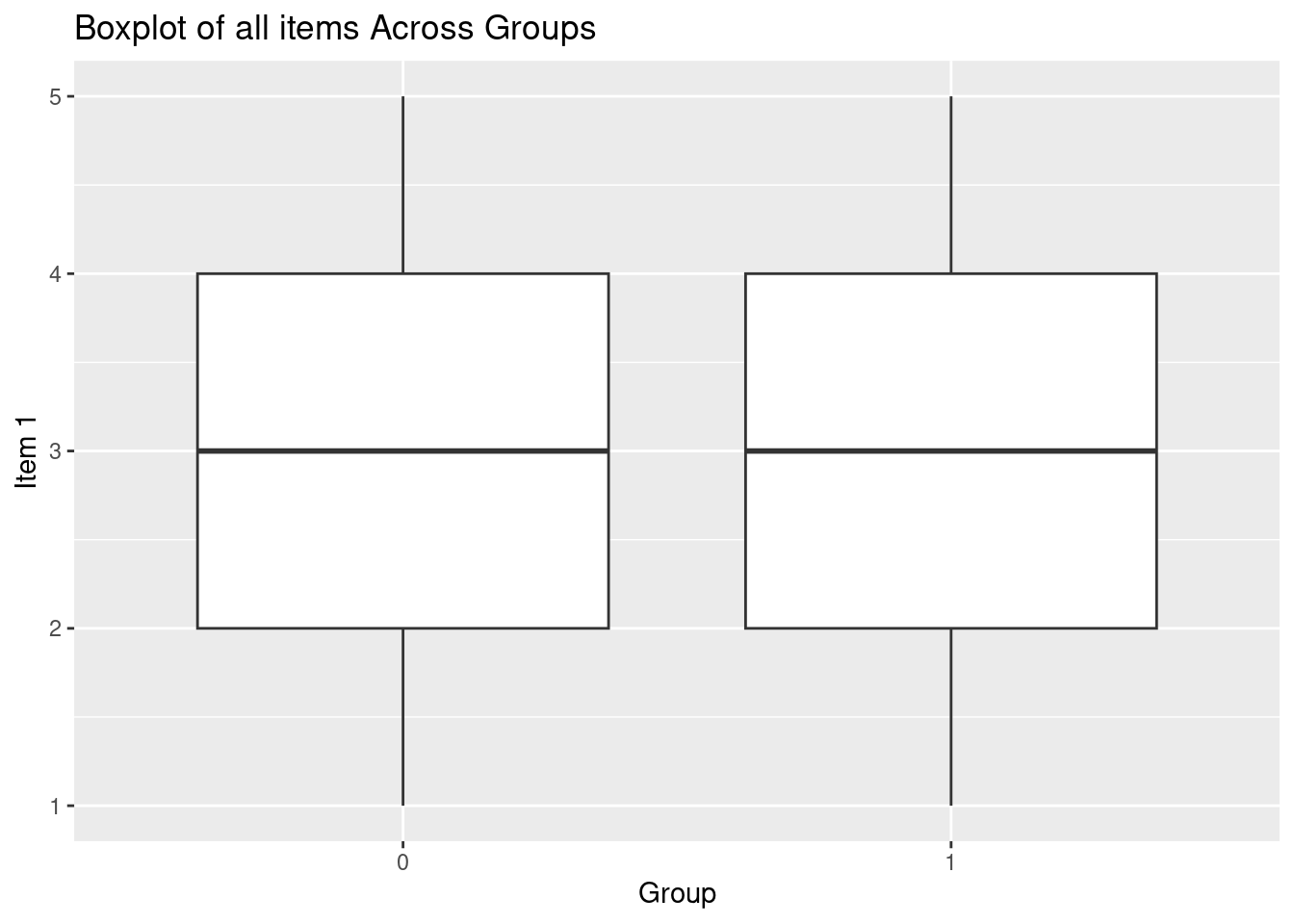
ggplot(df_test_long, aes(x = factor(group), y = value)) +
  geom_boxplot() +
  labs(x = "Group", y = "Item 1") +
  ggtitle("Boxplot of all items Across Groups")

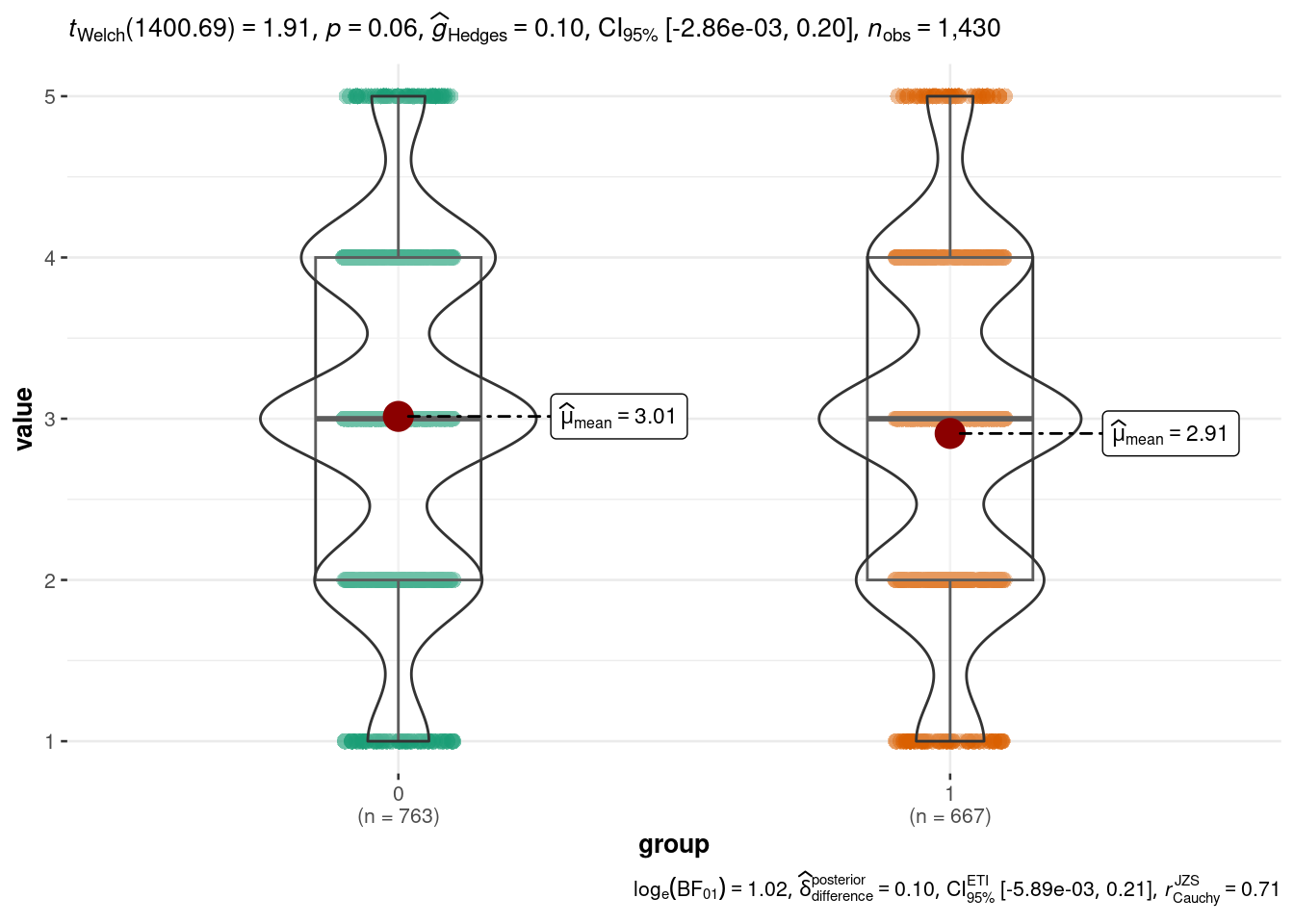
ggbetweenstats(
  data = df_test_long,
  x = group,
  y = value
)


# ##########################
# Prüfung der Normalitätsannahme
# ##########################

## Mit Shapiro
df_test |> 
  group_by(group) |> 
  shapiro_test(item_1)

## Mit QQ-Plots
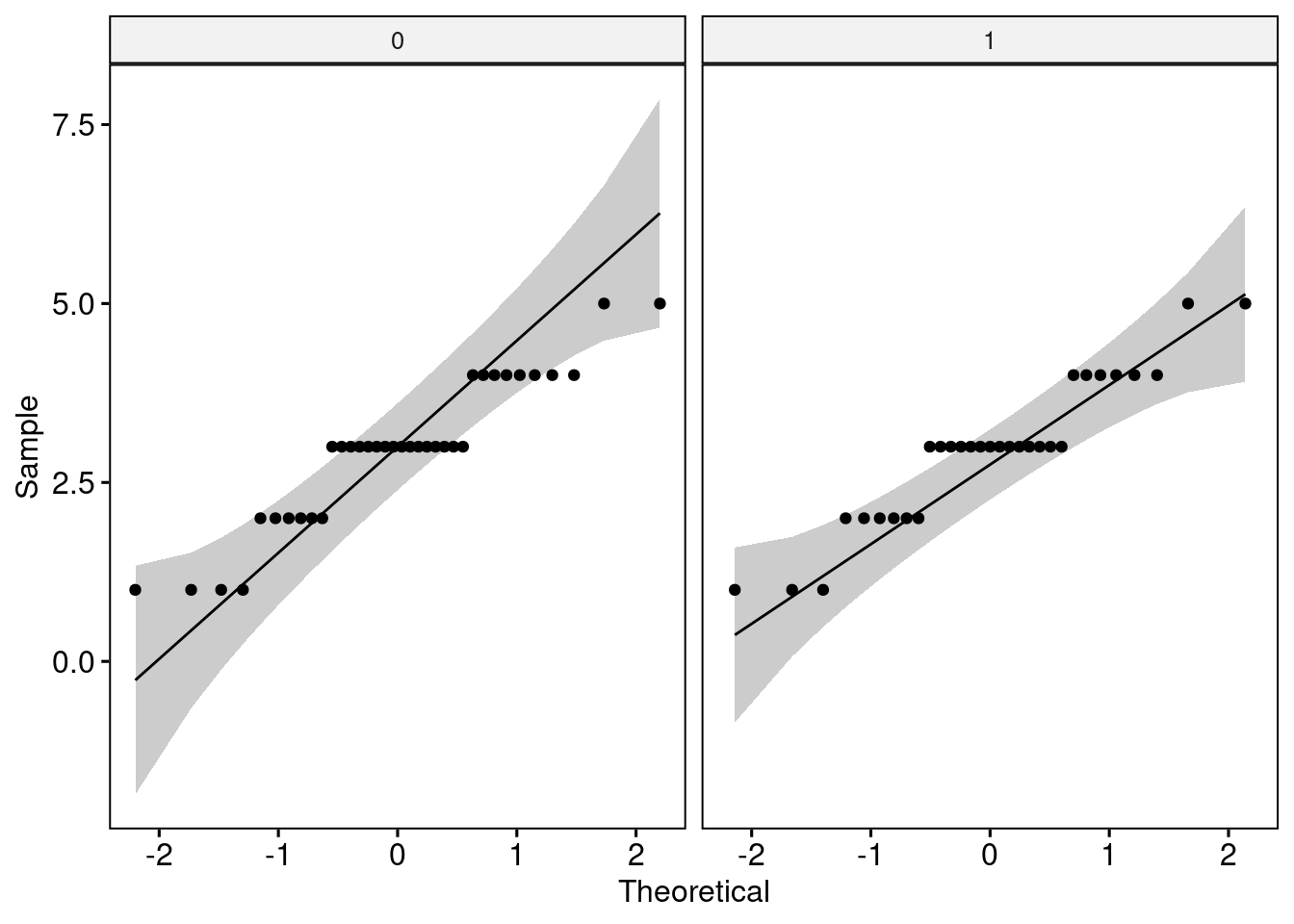
ggqqplot(df_test, x = "item_1", facet.by = "group")

# Wenn der p-Wert klein ist, müssen wir einen Test verwenden, der keine Normalverteilung annimmt 
# --> Mann-Whitney-U-Test (auch Wilcoxon-Rangsummentest genannt) vergleicht die Mediane 
# von zwei unabhängigen Gruppen und ist robust gegenüber 
# Nicht-Normalverteilung und unterschiedlichen Varianzen.

# ##########################
# Überprüfung der Varianzhomogenität
# ##########################

## Mit Levene
leveneTest(item_1 ~ as.character(group), data = df_test)

## Mit bartlett.test
bartlett.test(item_1 ~ group, data = df_test)

## Mit Fligner-Kelleen
fligner.test(item_1 ~ group, data = df_test)

# Wenn der p-Wert klein ist, ist die Varianz zwischen den Gruppen unterschiedlich und 
# wir müssen einen Test verwenden, der keine Normalverteilung annimmt 
# --> Welch-t-Test (oder Mann-Whitney)

# ##########################
# Test 
# ##########################

## Wenn Normalitäts- und Varianzannahmen erfüllt sind:
t.test(item_1 ~ group, data = df_test, var.equal = TRUE)

## Wenn Normalität erfüllt ist und Varianz nicht:
t.test(item_1 ~ group, data = df_test, var.equal = FALSE)

## Wenn Normalität nicht erfüllt ist:
wilcox.test(item_1 ~ group, data = df_test)

Hier ist der Inhalt des Skriptes und der R-Output zu sehen:

## ----echo=TRUE, message=FALSE-----------------------------------------------
if (!require(pacman)) install.packages("pacman")
pacman::p_load(tidyverse, janitor, psych, tinytable, ggstats, car, ggstatsplot, 
               modelsummary, knitr, kableExtra, ggpubr, rstatix, rempsyc)
rm(list = ls())

load("~/Dropbox/hsf/github/ewa/ss_24/read_in_71/data_71.RData")

# Zuerst wandle ich die Daten etwas um, so dass ich keine Faktorvariable mehr habe:
df_test <- df_cleaned |> 
  mutate_at(vars(starts_with("item_")), as.numeric)

# ##########################
# Ein-Stichproben t-Test
# ##########################

t.test(df_test$item_1, mu = 1)


    One Sample t-test

data:  df_test$item_1
t = 15.448, df = 66, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 1
95 percent confidence interval:
 2.689525 3.191072
sample estimates:
mean of x 
 2.940299

t.test(df_test$item_1, mu = 3)


    One Sample t-test

data:  df_test$item_1
t = -0.47532, df = 66, p-value = 0.6361
alternative hypothesis: true mean is not equal to 3
95 percent confidence interval:
 2.689525 3.191072
sample estimates:
mean of x 
 2.940299

# Standardmäßig führt t.test einen zweiseitigen Test durch:
t.test(df_test$item_1, mu = 3, alternative = "two.sided")


    One Sample t-test

data:  df_test$item_1
t = -0.47532, df = 66, p-value = 0.6361
alternative hypothesis: true mean is not equal to 3
95 percent confidence interval:
 2.689525 3.191072
sample estimates:
mean of x 
 2.940299

# Sie können einen Test für einen Teil der Daten durchführen, indem Sie ein Argument der t.test-Funktion verwenden:
t.test(df_test$item_1, 
       mu = 3, 
       alternative = "two.sided",
       subset(df_test, group == 0))


    Welch Two Sample t-test

data:  df_test$item_1 and subset(df_test, group == 0)
t = -14.256, df = 674.05, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 3
95 percent confidence interval:
 -1.02438061 -0.05000914
sample estimates:
mean of x mean of y 
 2.940299  3.477493

t.test(df_test$item_1, 
       mu = 3,
       alternative = "greater")


    One Sample t-test

data:  df_test$item_1
t = -0.47532, df = 66, p-value = 0.6819
alternative hypothesis: true mean is greater than 3
95 percent confidence interval:
 2.73076     Inf
sample estimates:
mean of x 
 2.940299

t.test(df_test$item_1, 
       mu = 3,
       alternative = "less")


    One Sample t-test

data:  df_test$item_1
t = -0.47532, df = 66, p-value = 0.3181
alternative hypothesis: true mean is less than 3
95 percent confidence interval:
     -Inf 3.149837
sample estimates:
mean of x 
 2.940299

# ##########################
# Zweiseitiger t-Test in R
# ##########################

# ----------------------------
# Für Daten im Breitformat:
# ----------------------------

# Welch-Test
t.test(df_test$item_1, df_test$item_2, data = df_test)


    Welch Two Sample t-test

data:  df_test$item_1 and df_test$item_2
t = 0.5873, df = 132.42, p-value = 0.558
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.2361367  0.4355743
sample estimates:
mean of x mean of y 
 2.940299  2.840580

# Student's t-Test
t.test(df_test$item_1, df_test$item_2, data = df_test, var.equal = TRUE)


    Two Sample t-test

data:  df_test$item_1 and df_test$item_2
t = 0.588, df = 134, p-value = 0.5575
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.2357030  0.4351406
sample estimates:
mean of x mean of y 
 2.940299  2.840580

# Welch-Test
t.test(df_test$item_1, df_test$item_2, data = df_test, 
       paired = TRUE, 
       var.equal = TRUE)


    Paired t-test

data:  df_test$item_1 and df_test$item_2
t = 0.71556, df = 66, p-value = 0.4768
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -0.1870352  0.3959904
sample estimates:
mean difference 
      0.1044776

## Die Antworten kommen von der selben Person, daher paired = TRUE

# ----------------------------
# Für Daten im Langformat:
# ----------------------------

# Test, ob das item_1 in beiden Gruppen gleich ist

# Erstelle ein Boxplot von item_1 über Gruppen mit ggplot2
ggplot(df_test, aes(x = factor(group), y = item_1)) +
  geom_boxplot() +
  labs(x = "Group", y = "Item 1") +
  ggtitle("Boxplot of Item 1 Across Groups")

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_boxplot()`).

ggbetweenstats(
  data = df_test,
  x = group,
  y = item_1
)

## Wenn Normalitäts- und Varianzannahmen erfüllt sind:
t.test(item_1 ~ group, data = df_test, var.equal = FALSE)


    Welch Two Sample t-test

data:  item_1 by group
t = 0.035326, df = 63.704, p-value = 0.9719
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -0.4978170  0.5157382
sample estimates:
mean in group 0 mean in group 1 
       2.944444        2.935484

# OK, aber wie testet man nun,
# ob die Antworten aller items in den jeweiligen Gruppen gleich sind? 

# Zuerst empfiehlt sich eine Umwandlung in das Langformat:
df_test_long <- df_test |> 
  pivot_longer(cols = starts_with("item_"), # Zu pivotierende Spalten
               names_to = "item",           # Neue Spalte für die Namen der Items
               values_to = "value")  |>     # Neue Spalte für die Werte der Items
  select(id, group, complete, item, value)

# Erstelle ein Boxplot von value über Gruppen mit ggplot2
ggplot(df_test_long, aes(x = factor(group), y = value)) +
  geom_boxplot() +
  labs(x = "Group", y = "Item 1") +
  ggtitle("Boxplot of all items Across Groups")

Warning: Removed 19 rows containing non-finite outside the scale range
(`stat_boxplot()`).

ggbetweenstats(
  data = df_test_long,
  x = group,
  y = value
)

# ##########################
# Prüfung der Normalitätsannahme
# ##########################

## Mit Shapiro
df_test |> 
  group_by(group) |> 
  shapiro_test(item_1)

# A tibble: 2 × 4
  group variable statistic       p
  <int> <chr>        <dbl>   <dbl>
1     0 item_1       0.903 0.00415
2     1 item_1       0.909 0.0121

## Mit QQ-Plots
ggqqplot(df_test, x = "item_1", facet.by = "group")

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_qq()`).

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_qq_line()`).
Removed 2 rows containing non-finite outside the scale range
(`stat_qq_line()`).

# Wenn der p-Wert klein ist, müssen wir einen Test verwenden, der keine Normalverteilung annimmt 
# --> Mann-Whitney-U-Test (auch Wilcoxon-Rangsummentest genannt) vergleicht die Mediane 
# von zwei unabhängigen Gruppen und ist robust gegenüber 
# Nicht-Normalverteilung und unterschiedlichen Varianzen.

# ##########################
# Überprüfung der Varianzhomogenität
# ##########################

## Mit Levene
leveneTest(item_1 ~ as.character(group), data = df_test)

Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1  0.0048 0.9451
      65

## Mit bartlett.test
bartlett.test(item_1 ~ group, data = df_test)


    Bartlett test of homogeneity of variances

data:  item_1 by group
Bartlett's K-squared = 0.0028132, df = 1, p-value = 0.9577

## Mit Fligner-Kelleen
fligner.test(item_1 ~ group, data = df_test)


    Fligner-Killeen test of homogeneity of variances

data:  item_1 by group
Fligner-Killeen:med chi-squared = 0.0049046, df = 1, p-value = 0.9442

# Wenn der p-Wert klein ist, ist die Varianz zwischen den Gruppen unterschiedlich und 
# wir müssen einen Test verwenden, der keine Normalverteilung annimmt 
# --> Welch-t-Test (oder Mann-Whitney)

# ##########################
# Test 
# ##########################

## Wenn Normalitäts- und Varianzannahmen erfüllt sind:
t.test(item_1 ~ group, data = df_test, var.equal = TRUE)


    Two Sample t-test

data:  item_1 by group
t = 0.035301, df = 65, p-value = 0.9719
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -0.4979828  0.5159040
sample estimates:
mean in group 0 mean in group 1 
       2.944444        2.935484

## Wenn Normalität erfüllt ist und Varianz nicht:
t.test(item_1 ~ group, data = df_test, var.equal = FALSE)


    Welch Two Sample t-test

data:  item_1 by group
t = 0.035326, df = 63.704, p-value = 0.9719
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -0.4978170  0.5157382
sample estimates:
mean in group 0 mean in group 1 
       2.944444        2.935484

## Wenn Normalität nicht erfüllt ist:
wilcox.test(item_1 ~ group, data = df_test)

Warning in wilcox.test.default(x = DATA[[1L]], y = DATA[[2L]], ...): cannot
compute exact p-value with ties


    Wilcoxon rank sum test with continuity correction

data:  item_1 by group
W = 566, p-value = 0.9206
alternative hypothesis: true location shift is not equal to 0