8 Games

Game theory is the study of mathematical models that describe strategic interactions among rational decision-makers. Specifically, it analyzes how two or more players make decisions in situations where their choices affect one another’s outcomes. In these scenarios, each player’s actions influence the payoffs of others, and vice versa, creating interdependence. As in the models discussed earlier, game theory assumes that players act rationally, seeking to maximize their own benefits. This framework allows for economic research through laboratory experiments or real-world field studies.

Game theory is not just an academic exercise; it has practical applications in real market situations and various human interactions. It is used across all fields of science including social science and computer science. In the 21st century, game theory has expanded to cover a wide range of behavioral relationships and is now an umbrella term for the study of logical decision-making in humans, animals, and machines.

Figure 8.1: The book of Von Neumann & Morgenstern (1947)

Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. His work and in particular his jointly written with Oskar Morgenstern from 1944 Theory of Games and Economic Behavior (see Figure 8.1) which considered cooperative games of several players was the beginning of modern game theory. The second edition of this book provided an axiomatic theory of expected utility, which allowed mathematical statisticians and economists to treat decision-making under uncertainty.

Figure 8.2: Nobel price winners that contributed to game theory

Game theory has been widely recognized as an important tool in many fields. As of 2014, with the Nobel Memorial Prize in Economic Sciences going to game theorist Jean Tirole, eleven game theorists have won the economics Nobel Prize including Reinhard Selten from Germany together with John Harsanyi and John Nash in 1994, see Figure 8.2.

Exercise 8.1 The dissertation of John Nash

Discuss: How many citations does a good academic work require?
Read Nash (1950) and discuss the question once again. The dissertation is available here.

Solution

The reference list in John Nash’s doctoral thesis Nash (1950) contains only two entries (see Figure 8.3): the book by Von Neumann & Morgenstern (1947) and a short note from his own publication. His thesis, along with several other works, earned him the Nobel Prize, the Abel Prize, and other prestigious honors.

Figure 8.3: Reference list of Nash (1950)

Nash, J. F. (1950). Non-cooperative games [PhD thesis]. Princeton University Princeton.

Von Neumann, J., & Morgenstern, O. (1947). Theory of games and economic behavior. Princeton University Press.

8.1 Structure of games

8.1.1 Elements

The elements of a game include several key components that define its structure and dynamics. First, there is the number of players, which indicates how many individuals or entities are involved in the game. Each player has a specific set of strategies and alternative actions available to them, which can significantly influence the game’s outcome.

Additionally, the payoff functions determine the rewards or penalties that players receive based on the actions taken, reflecting their preferences and objectives. The state of information is also crucial, as it outlines what each player knows about the game, including the actions of other players. Lastly, the timing of actions and information plays a vital role, as it affects the decisions made by players and the overall flow of the game. Understanding these elements is essential for analyzing strategic interactions effectively.

8.1.2 Classes

Games can be categorized into various classes based on their characteristics:

Cooperative vs. Non-cooperative: Cooperative games allow players to form binding commitments, while non-cooperative games do not.
Static vs. Dynamic: Static games are played in a single time period, whereas dynamic games unfold over multiple periods, with players potentially adapting their strategies over time.
One-shot vs. Repeated: One-shot games are played once, while repeated games involve the same players playing multiple rounds, allowing for strategy adjustments based on previous outcomes.
Non-zero-sum vs. Zero-sum: In zero-sum games, one player’s gain is another’s loss, while non-zero-sum games allow for outcomes where all players can benefit or suffer together.
Perfect Information vs. Non-perfect Information: Perfect information games allow players to know all previous actions, whereas non-perfect information games involve some level of uncertainty about other players’ actions.
Symmetric Information vs. Asymmetric Information: In symmetric information games, all players have access to the same information, while asymmetric information games involve players having different information.
Deterministic vs. Non-deterministic Payoffs (Random): Deterministic payoffs yield consistent outcomes for given strategies, while non-deterministic payoffs involve randomness and variability in outcomes.

Exercise 8.2 Tic Tac Toe

Tic Tac Toe is a simple yet classic game that can be analyzed through various game theory classifications. Discuss the classes of the game Tic Tac Toe (see Figure 8.4).

Solution

Here’s how it fits into the categories mentioned:

Cooperative vs. Non-cooperative:
Non-cooperative: Tic Tac Toe is a non-cooperative game because players cannot form binding agreements or commitments. Each player independently decides their move without collaboration.

Static vs. Dynamic:
Dynamic: The game is dynamic because it occurs in various rounds, with players taking turns one after another and they have the chance to respond on the moves made by the opponent.

One-shot vs. Repeated:
One-shot: A typical game of Tic Tac Toe is a one-shot game, meaning it is played once with no subsequent rounds. However, players may play multiple games in sequence, which can lead to a repeated game scenario, but each individual game remains one-shot.

Non-zero-sum vs. Zero-sum:
Zero-sum: Tic Tac Toe is a zero-sum game because one player’s gain (winning the game) results in an equal loss for the other player.

Perfect Information vs. Non-perfect Information:
Perfect Information: The game has perfect information as both players are fully aware of all previous moves made by their opponent. There is no hidden information; each player can see the entire game board and all actions taken.

Symmetric Information vs. Asymmetric Information:
Symmetric Information: The game exhibits symmetric information, where both players have access to the same information regarding the game’s state. They both see the same board and the same moves, and neither player has an informational advantage over the other.

Deterministic vs. Non-deterministic Payoffs:
Deterministic: The payoffs in Tic Tac Toe are deterministic, as the outcome (win, loss, or draw) is solely determined by the players’ moves without any random elements involved. Each strategic decision directly influences the final result.

8.1.3 Representations

8.1.3.1 Normal form

The normal form of a game is a matrix representation that captures the strategic interactions between players who choose their strategies simultaneously. It lists each player’s possible strategies and the resulting payoffs for each combination of strategies. This format helps identify dominant strategies and Nash equilibria, making it useful for analyzing static games.

The matrix provided in Table 8.1 is a normal-form representation of a game in which players move simultaneously (or at least do not observe the other player’s move before making their own) and receive the payoffs as specified for the combinations of actions played.

Table 8.1: Example of a normal-form representation

		Person B - work	Person B - shirk
Person A - work	10 ; 10	5 ; 11
Person A - shirk	11 ; 5	6 ; 6

In the example of Table 8.1, two workers, A and B, have to make the choice to shirk or to work hard. In the following, I describe how to solve the decision for each person. The trick is to find the best answer of each person in whatever the other one is doing.

To solve the game represented in the normal-form table, follow these steps:

Identify strategies: Each player (Person A and Person B) has two strategies: “work” or “shirk.”
Payoff matrix: The matrix shows the payoffs for both players based on their chosen strategies:
- If both work, the payoffs are (10, 10).
- If A works and B shirks, the payoffs are (5, 11).
- If A shirks and B works, the payoffs are (11, 5).
- If both shirk, the payoffs are (6, 6).
Determine dominant strategies: A dominant strategy is one that yields a higher payoff regardless of the other player’s action.

For Person A:

If B works, A gets 10 by working and 11 by shirking (so shirking is better).
If B shirks, A gets 5 by working and 6 by shirking (so again, shirking is better).
Thus, A’s dominant strategy is to shirk.

For Person B:

If A works, B gets 10 by working and 11 by shirking (so shirking is better).
If A shirks, B gets 5 by working and 6 by shirking (so again, shirking is better).
Thus, B’s dominant strategy is to shirk.

Nash Equilibrium: The Nash equilibrium occurs when both players choose their dominant strategies. In this case, both will choose to shirk: Payoffs at this equilibrium are (6, 6).
Conclusion: Both players have a strong incentive to shirk, leading to a Nash equilibrium with both receiving a payoff of 6.

This analysis shows how rational decision-making can lead to outcomes that may not be optimal for either player collectively, highlighting the potential for suboptimal outcomes in strategic interactions.

Exercise 8.3 Matching pennies (random and simultaneous version)

Write down the following game in the normal form:

Matching pennies (random and simultaneous version) is a game with two players (1, 2). Both players flip a penny simultaneously. Each penny falls down and shows either heads up or tails up. If the two pennies match (either both heads up or both tails up), player 2 wins and player 1 must pay him a Euro. If the two pennies do not match, player 1 wins and player 2 must pay him a Euro.

Additionally, describe the elements of the game and the class of this game.

Solution

The normal form of the game is shown in Table 8.2.

Table 8.2: Normal form of the random and simultaneous version

		Person 2 - Head	Person 2 - Tail
Person 1 - Head	-1 ; 1	1 ; -1
Person 1 - Tail	1 ; -1	-1 ; 1

It is a game that belongs to the following classes:

non-cooperative
static
one-shot
zero-sum
perfect information
symmetric information
non-deterministic payoffs

Elements of the game:

Number of players: 2
Number of strategies: No strategies as whether heads or tails shows up is random
Payoff functions: \[ \text{Player 1} = \begin{cases} 1, & \text{if } (T,T) \text{ or } (H,H) \\ -1, & \text{otherwise} \end{cases} \]

\[ \text{Player 2 = } \begin{cases} 1, & \text{if } (H,T) \text{ or } (T,H) \\ -1, & \text{otherwise} \end{cases} \]

State of information: Everybody knows the rules and is perfectly informed
Timing of actions and information: both throw the coin at the same time and see the result at the same time

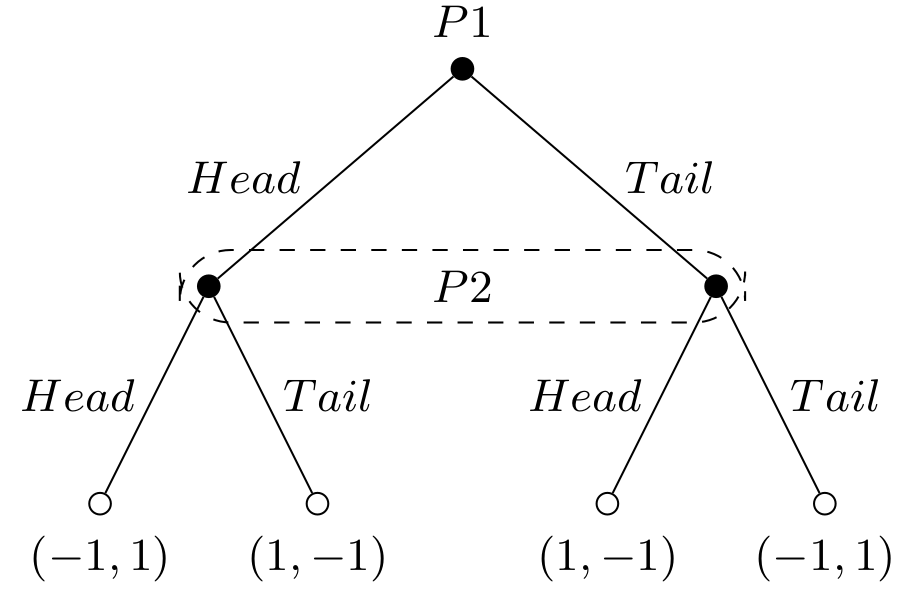
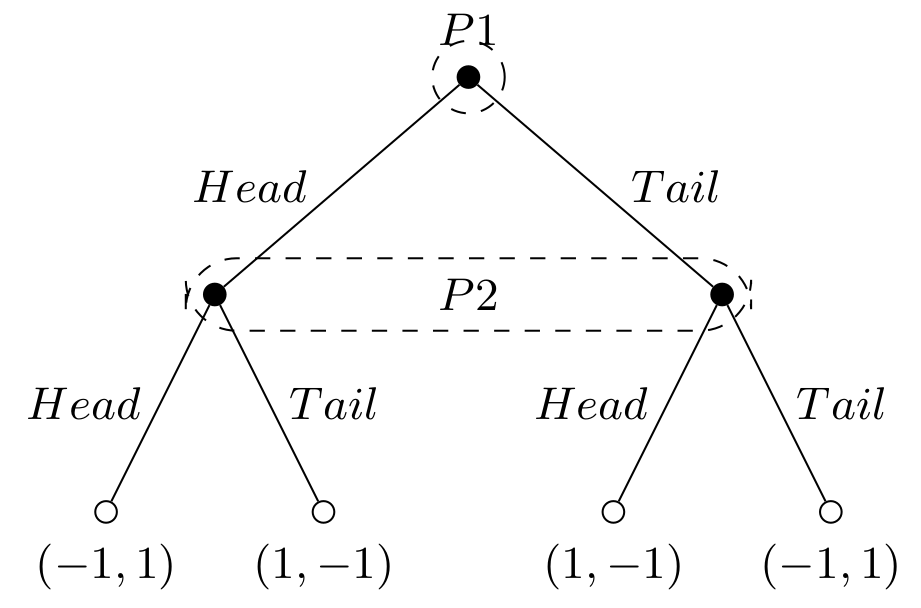
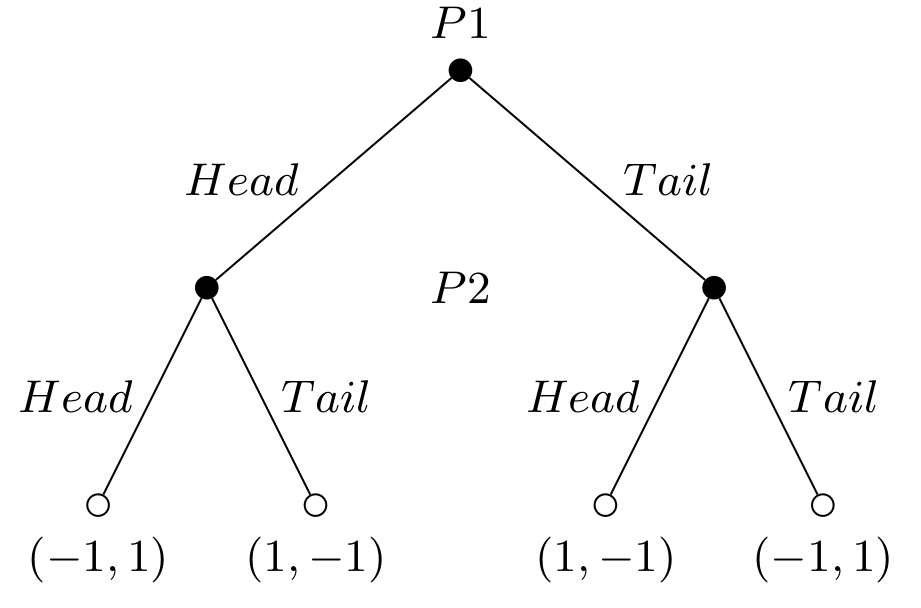
8.1.4 Extensive form

The extensive form in game theory is a way to represent games that captures the sequence of moves by players, their available choices at each point, and the information they have when making decisions. Unlike the normal form, which shows all strategies and payoffs in a matrix, the extensive form uses a tree diagram to show how a game unfolds over time. Each branch represents a possible action, and the endpoints show the payoffs for different outcomes. This format also accounts for chance events and imperfect information, making it useful for analyzing dynamic, sequential decision-making scenarios.

Exercise 8.4 Matching pennies (random version)

Write down the following game in the extensive form:

Matching pennies (random version) is a game with two players (1, 2). Player 1 starts by flipping a fair penny high, catches it, and then turns it over into the other hand so that the result is hidden from the other player. Then, player 2 flips the coin. If the two pennies match (either both heads up or both tails up), player 2 wins and player 1 must pay him a Euro. If the two pennies do not match, player 1 wins and player 2 must pay him a Euro.

Solution

As player 2 has no idea what player 1 has chosen, he cannot come up with any strategy that increases his winning rate. The extensive

Figure 8.5: Extensive form of the random version

The dashed circled line indicates that player 2 is not informed about whether P1 decided head or tail. As we have now introduced how to graphically show that some players have a restricted information set, we can draw the extensive form also for the random and simultaneous version of the matching pennies game. Please note that the dashed circle around player 1 is redundant and hence it is a convention not to draw it sometimes.

Figure 8.6: Extensive form of the random and simultaneous version

Exercise 8.5 Matching pennies (strategic version)

Write down the following game in the extensive form and discuss the strategies of both:

Matching pennies (strategic version) is a game with two players (1, 2). Player 1 starts and decides whether to put a coin with either heads up or tails up onto a table. Player 2 can see the decision of player 1. Then, player 2 decides whether to put a coin with heads or tails on the table. If the two pennies match (either both heads up or both tails up), player 2 wins and player 1 must pay him a Euro. If the two pennies do not match, player 1 wins and player 2 must pay him a Euro.

Solution

As player 2 has complete information about the decision of player 1, he can always come up with the choice that makes him win. That is, if player 1 chooses head(/tail) player one will also choose head(/tail).

Figure 8.7: Extensive form of the strategic version

8.2 Nash equilibrium

8.2.1 John Forbes Nash Jr. (1928-2015)

John Forbes Nash Jr. (1928-2015) had an extraordinary life which ended tragically in a car accident after having received the Abel Prize. In Figure 8.8 you see the real John Nash as well as actor Russel Crowe who plays him in the movie A Beautiful Mind. To get known to John Nash and his contributions, read his Wikipedia entry, watch the following videos, and read the Nobel prize award ceremony speech below.

Nash Equilibrium (taken from A Beautiful Mind)

Dr. John Nash on his life before and after the Nobel Prize

Figure 8.8: John Nash and The Beautiful Mind movie

Nobel Prize Award ceremony speech of 1994

Presentation Speech by Professor Karl-Göran Mäler of the Royal Swedish Academy of Sciences taken from Nobel Prize Speech):

Many situations in society, from everyday life to high-level politics, are characterized by what economists call strategic interactions. When there is strategic interaction, the outcome for one agent depends not only on what that agent does, but also very largely on how other agents act or react. A firm that decreases its price to attract more customers will not succeed in this strategy if the other major firms in the market use the same strategy. Whether a political party will be successful in attracting more votes by proposing lower taxes or increased spending will depend on the proposals from other parties. The success of’ a central bank which is trying to fight inflation by maintaining a fixed exchange rate depends – as we know – on decisions on fiscal policy, and also on reactions in markets for labor and commodities.

A simple economic example of strategic interaction is where two firms are competing with identical products on the same market. If one firm increases its production, this will make the market price fall and therefore reduce profits for the other firm. The other firm will obviously try to counteract this, for example by increasing its production and so maintaining its market share but at the cost of further reduction in market price. The first company must therefore anticipate this countermove and possible further countermoves when it makes its decision to increase production. Can we predict how the parties will choose their strategies in situations like this?

As early as the 1830s the French economist Auguste Cournot had studied the probable outcome when two firms compete in the same market. Many economists and social scientists subsequently tried to analyze the outcome in other specific forms of strategic interaction. However, prior to the birth of game theory, there was no toolbox that gave scholars access to a general but rigorous method of analyzing different forms of strategic interaction. The situation is totally different now. Scientific journals and advanced textbooks are filled with analyses that build on game theory, as it has been developed by this year’s Laureates in economics, John Nash, John Harsanyi and Reinhard Selten.

Non-cooperative game theory deals with situations where the parties cannot make binding agreements. Even in very complicated games, with many parties and many available strategies, it will be possible to describe the outcome in terms of a so-called Nash equilibrium – so named after one of the Laureates. John Nash has shown that there is at least one stable outcome, that is an outcome such that no player can improve his own outcome by choosing a different strategy when all players have correct expectations of each other’s strategy. Even if each party acts in an individually rational way, the Nash equilibrium shows that strategic interaction can quite often cause collective irrationality: trade wars or excessive emission of pollutants that threaten the global environment are examples in the international sphere. One should also add that the Nash equilibrium has been important within evolutionary ecology – to describe natural selection as a strategic interaction within and between species.

In many games, the players lack complete information about each other’`s objective. If the government, for example, wants to deregulate a firm but does not know the cost situation in the firm, while the firm’s management has this knowledge, we have a game with incomplete information. In three articles published toward the end of the 1960s, John Harsanyi showed how equilibrium analysis could be extended to handle this difficulty, which game theorists up to that time had regarded as insurmountable. Harsanyi’s approach has laid an analytical basis for several lively research areas including information economics which starts from the fact that different decision makers, in a market or within an organization, often have access to different information. These areas cover a broad range of issues, from contracts between shareholders and a company’s management to institutions in developing countries.

One problem connected with the concept of Nash equilibrium is that there may be several equilibria in non-cooperative games. It may thus be difficult – both for the players and an outside analyst – to predict the outcome. Reinhard Selten has, through his ``perfection’’ concepts, laid the foundations for the research program that has tried to exclude improbable or unreasonable equilibria. Certain Nash equilibria can, in fact, be such that they are based on threats or promises intended to make other players choose certain strategies. These threats and promises are often empty because it is not in the player’s interest to carry them out if a situation arises in which he has threatened to carry them out. By excluding such empty threats and promises Selten could make stronger predictions about the outcome in the form of socalled perfect equilibria.

Selten’s contributions have had great importance for analysis of the dynamics of strategic interaction, for example between firms trying to reach dominant positions on the market, or between private agents and a government that tries to implement a particular economic policy.

Professor John Harsanyi, the analysis of games with incomplete information is due to you, and it has been of great importance for the economics of information.

Dr John Nash, your analysis of equilibria in non-cooperative games, and all your other contributions to game theory, have had a profound effect on the way economic theory has developed in the last two decades. Professor Reinhard Selten, your notion of perfection in the equilibrium analysis has substantially extended the use of non-cooperative game theory.

It is an honour and a privilege for me to convey to all of you, on behalf of the Royal Swedish Academy of Sciences, our warmest congratulations. I now ask you to receive your prizes from the hands of his Majesty the King.

8.2.2 Nash equilibrium

To find a Nash equilibrium in a normal form game as shown in Table 8.3, we can look for the best responses for both players in a game. We do so by putting a star next to the payoff attained by the best response of a player for all the strategies of the other player. For example, we put a star next to the 4 because S1 is the best response by Player B to the action S1 of Player A.

Notice that the bottom right corner box has a particular feature: it shows that the strategies played by all the (two) players and resulting in that outcome are best responses to the others’ players best responses. That defines a Nash equilibrium.

Table 8.3: An example for a game with a Nash equilibrium

		Person B
		S1	S2	S3
Person A	S1	0 ; 4*	4* ; 0	5 ; 3
	S2	4* ; 0	0 ; 4*	5 ; 3
	S3	3 ; 5	3 ; 5	6* ; 6*

Nash equilibrium

The Nash equilibrium is a concept of game theory where the optimal outcome of a game is one where no player has an incentive to deviate from their chosen strategy after considering the opponent’s choice.

Please watch the video: What is Nash Equilibrium?

8.2.3 The prisoner’s dilemma

The prisoner’s dilemma is the most well-known example of game theory. It shows why two completely rational individuals might not cooperate, even if it appears that it is in their best interests to do so.

Consider the example of two criminals arrested for a crime. Prosecutors have no hard evidence to convict them. However, to gain a confession, officials remove the prisoners from their solitary cells and question each one in separate chambers. Neither prisoner has the means to communicate with each other. The criminals are now confronted by the officials with four possible scenarios:

If both confess, they will each receive an eight-year prison sentence.
If Prisoner 1 confesses, but Prisoner 2 does not (he aims to cooperate with Prisoner 1), Prisoner 1 will go free and Prisoner 2 will get twenty years.
If Prisoner 2 confesses, but Prisoner 1 does not (he aims to cooperate with Prisoner 1), Prisoner 1 will get twenty years, and Prisoner 2 will go free.
If neither confesses, each will serve two years in prison.

The corresponding normal form of the game is shown in Table 8.4.

Table 8.4: Example for a prisoner’s dilemma

		Person B
		Confess	Cooperate
Person A	Confess	8 years ; 8 years	0 years ; 20 years
	Cooperate	20 years ; 0 years	2 years ; 2 years

The scenario is also explained in this video

Let us now look at how individuals would rationally decide what to do:

If A assumes that B confesses, A would also confess.
If A assumes that B cooperates, A would still confess.

Since the same logic applies for B, we can conclude that the strategy of choice is to confess, even though the most favorable strategy for both would be to cooperate. The game-theoretical equilibrium (both confess) in this game can be called a Nash equilibrium because it suggests that both players will make the move that is best for them individually, even if it is worse for them collectively.

Exercise 8.6

Define briefly what is meant by a Nash equilibrium.
Analyze whether the normal form of the given game has a Nash equilibrium. Please notice that high numbers indicate high utility, ranging from \(0\) (no utility) to \(10\) (high utility).

Table 8.5: Normal form of a game

		Player 2
		P	V
Player 1	P	2, 4	2, 6
	V	7, 1	3, 3

Solution

The Nash equilibrium is a concept of game theory where the optimal outcome of a game is one where no player has an incentive to deviate from his chosen strategy after considering an opponent’s choice.
In the game above the point where both play with (3,3) is a Nash-Equilibrium Nash equilibrium.