12 Elasticity

Required reading: Shapiro et al. (2022, ch. 5)

Shapiro, D., MacDonald, D., & Greenlaw, S. A. (2022). Principles of economics (3rd ed.). OpenStax. https://openstax.org/details/books/principles-economics-3e

Learning objectives:

Students will be able to:

Explain the concept of price elasticity of demand and how to calculate it.
Describe what it means for demand to be price inelastic, unit price elastic, price elastic, perfectly price inelastic, and perfectly price elastic.
Explain how and why the value of price elasticity of demand changes along a linear demand curve.
Understand the relationship between total revenue and price elasticity of demand.

12.1 How to measure an elasticity

Elasticity is the measurement of the percentage change of one economic variable in response to a change in another. Here, elasticity refers to the degree to which individuals, consumers, or producers change their demand or the amount supplied in response to price or income changes. Elasticity is a normalized measure, meaning the units of measurement of the variables (€, cent, kg, g) do not play a role, enabling comparisons of how different goods react to price changes, for example.

The price elasticity of demand (PED) is computed as the percentage change in the quantity demanded divided by the percentage change in price:

\[ \text{PED} = \frac{\text{Percentage change in quantity demanded}}{\text{Percentage change in price}} = \frac{\frac{q_{t=\text{today}} - q_{t=\text{yesterday}}}{q_{t=\text{yesterday}}}}{\frac{p_{t=\text{today}} - p_{t=\text{yesterday}}}{p_{t=\text{yesterday}}}} \]

Exercise 12.1 How Rachel’s demand reacts to changes in price

Rachel’s demand curve is linear. Her demand decreases from 10 to 6 liters of milk if the price increases from 50 to 70 cents. Suppose you know that Rachel’s demand curve for cookies is also linear and that her demand decreases from 3 to 1 cookie if the price increases from 20 to 40 cents.

As the prices changed in both cases by 20 cents, can we say that she reacts more sensitively to prices of milk compared to cookies because she buys 4 units more of milk and just 2 units less of cookies?

Solution

No, we cannot conclude this without discussing elasticities. We would be comparing apples with pears, or in this case, cookies with milk, as the units of measurement are different.

Let’s calculate the elasticities:

Example milk: If the price of a liter of milk increases from €0.50 to €0.70, and the amount demanded falls from 10 to 6 liters, then the price elasticity of demand (PED) for milk is calculated as:

\[ PED_{milk}^*=\frac{\frac{6-10}{10}\cdot 100}{\frac{(\text{€}0.70 - \text{€}0.50)}{\text{€}0.50}\cdot 100} = -1 \]

Example cookie: If the price of a cookie increases from €0.20 to €0.40 and the amount demanded falls from 3 to 1 cookie, then the price elasticity of demand (PED) for cookies is:

\[ PED_{cookie}^*=\frac{\frac{1-3}{3}\cdot 100}{\frac{(\text{€}0.40-\text{€}0.20)}{\text{€}0.20}\cdot 100}=-\frac{2}{3} \]

This means if the price increases by 1%, Rachel will demand 1% less of milk and $\frac{2}{3}$% less of cookies. Thus, we can conclude that she is more price-sensitive to milk.

Exercise 12.2 Check for units of measurement and direction of change

Assume a cookie weighs 100g and we use $ as currency, with one dollar equal to €0.86. Recalculate the $PED_{cookie}$ using grams as the unit of measurement.
You may have heard that the problem with the simple method of calculation is that the precise magnitude of the elasticity depends on the direction of change. Thus, calculate the elasticities if the prices decrease from €0.70 to €0.50 and from €0.20 to €0.40, respectively. In other words, assume that quantities and prices from the earlier example change in the opposite direction.

Solution

Check: Units of Measurement
To convert €0.20 to $, calculate:

\[ \text{€}0.40 \cdot \frac{\text{\$}1}{\text{€}0.86} = \text{\$}0.465116279 \] and hence €0.20 = 0.23255814$. Then,

\[ PED_{cookie}^* = \frac{\frac{100g - 300g}{300g} \cdot 100}{\frac{(\text{\$}0.465116279 - \text{\$}0.23255814)}{\text{\$}0.23255814} \cdot 100} = -\frac{2}{3} \] Check: it remains the same.

Check: Direction of Change
\[ PED_{milk}^* = \frac{\frac{10 - 6}{6} \cdot 100}{\frac{(\text{€}0.50 - \text{€}0.70)}{\text{€}0.70} \cdot 100} = \frac{\frac{2}{3}}{\frac{2}{7}} = -\frac{7}{3} \]

\[ PED_{cookie}^* = \frac{\frac{3 - 1}{1} \cdot 100}{\frac{(\text{€}0.20 - \text{€}0.40)}{\text{€}0.40} \cdot 100} = -4 \]

The result is significantly different. Thus, this method of calculation is inadequate.
Solution: Midpoint Method, see ?sec-midpoint.

12.2 Midpoint method

The midpoint formula computes percentage changes by dividing the change by the average value (i.e., the midpoint) of the initial and final value. It is independent of the direction of change and hence is preferable to the basic method. For example, when a change in price from P_1 to P_2 comes along with a change in demand from Q_1 to Q_2, the formula can be written like this:

\[ \text{Price Elasticity of Demand (PED)} = \frac{\frac{Q_2 - Q_1}{\left(\frac{(Q_2 + Q_1)}{2}\right)}}{\frac{(P_2 - P_1)}{\left(\frac{(P_2 + P_1)}{2}\right)}} = \frac{\triangle Q / \bar{Q}}{\triangle P / \bar{P}} \]

Notice that the formula can be simplified by using the $\triangle$ symbol to represent a change in values, and using a bar over the quantities to indicate the average of the two values.

Exercise 12.3 Midpoint method and the direction of change

Check if applying the midpoint method is really a solution, i.e., the elasticities of milk and cookies are direction of change.

Solution

\[ PED_{milk} = \frac{\frac{10 - 6}{\frac{(10 + 6)}{2}}}{\frac{(\text{€}0.50 - \text{€}0.70)}{\frac{(\text{€}0.50 + \text{€}0.70)}{2}}} = -\frac{3}{2} = -1.5 \]

\[ PED_{milk} = \frac{\frac{6 - 10}{(6 + 10)/2}}{\frac{(0.70 - 0.50)}{(0.70 + 0.50)/2}} = -1.5 \\ \]

\[ PED_{cookie} = \frac{\frac{1 - 3}{4}}{\frac{(0.40 - 0.20)}{0.30}} = -0.375 \\ \]

\[ PED_{cookie} = \frac{\frac{3 - 1}{4}}{\frac{(0.20 - 0.40)}{0.30}} = -0.375 \]

Thus, a 1% increase in price will lead to a drop in quantity demanded of 1.5% for milk and 0.375% for cookies.

12.3 Point elasticity

More generally, we can use differential calculus to get the the elasticity of two variables, x and y: \[ \epsilon_{y,x} = \frac{d Q }{d P}\cdot \frac{P}{Q} \]

12.4 Elasticity and demand

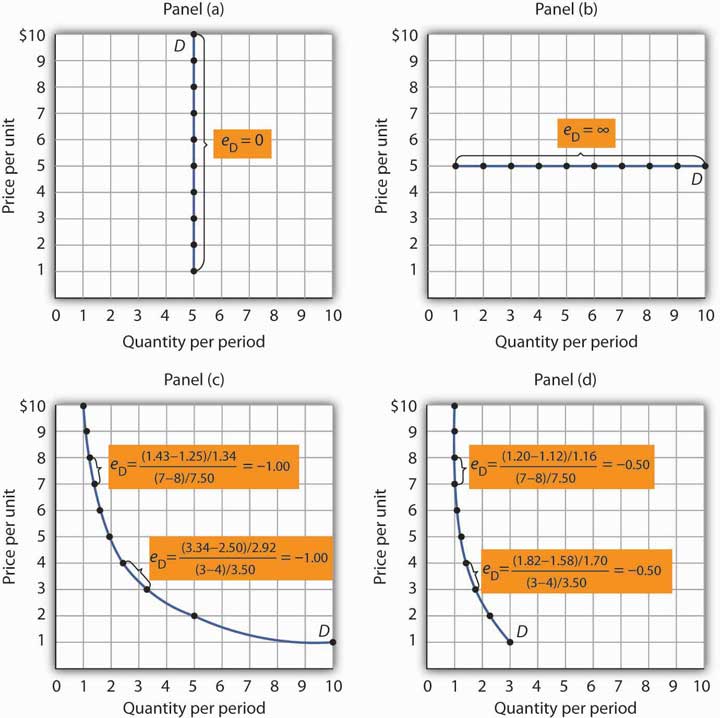
12.4.1 Terms: Elastic, Inelastic, Perfectly Elastic, and Perfectly Inelastic

Price elasticity of demand (PED) has various classifications that help us understand how quantity demanded responds to price changes. It is termed perfectly elastic when $|PED| \rightarrow \infty$, indicating that quantity responds infinitely to even the smallest price change. Conversely, it is labeled perfectly inelastic when $PED = 0$, signifying that quantity does not respond at all to price changes.

In less extreme cases, we refer to price inelastic demand when $0 < |PED| < 1$, meaning that quantity demanded does not respond significantly to changes in price. On the other hand, price elastic demand occurs when $|PED| > 1$, indicating a strong responsive relationship between quantity demanded and price.

Understanding PED is crucial as it measures the sensitivity of quantity demanded to price changes and is closely related to the slope of the demand curve. However, it is important to note that the slope alone does not provide the complete picture of PED.

Exercise 12.4 Sketch demand curves

Sketch demand curves for
- Normal goods with price inelastic demand
- Normal goods with perfect price inelastic demand
- Normal goods with price elastic demand
- Normal goods with perfect price elastic demand
Do the same for a Giffen good.

Determinants of PED: Several factors influence the price elasticity of demand. The availability of close substitutes plays a significant role, as does the classification of goods into necessities versus luxuries. Additionally, the time horizon can impact elasticity.

Price elasticity of a linear demand curve {#sec-slopedemand}:

When examining the price elasticity of a linear demand curve, it is essential to recognize that while the slope remains constant, elasticity does not! Demand is typically inelastic at points with low prices and high quantities, whereas it becomes elastic at points with high prices and low quantities. This is demonstrated in Figure 12.1 and Figure 12.2.

Moreover, total revenue varies at each point along the demand curve. Demand curves with a constant price elasticity are referred to as iso-elastic. An iso-elastic demand curve is shown in panel (c) of Figure 12.1.

Figure 12.1: Representations of different PEDs

Figure 12.2: Price elasticities of demand for a linear demand curve