25 Financial market

Learning objectives:

Students will be able to:

Understand the basic functioning of the money market.
Recognize that money supply and money demand determine the interest rate.
Explain how central banks influence money demand by influencing the interest rate.
Analyze the effects of a monetary expansion.
Derive the building blocks of our short-run model: the LM-curve.

Required readings:
Blanchard & Johnson (2013, ch. 5).

Recommended readings: Blanchard & Johnson (2013, ch. 4).

25.1 Semantic traps: Money, income, and wealth

Words such as money or wealth have specific meanings in economics, which differ from their everyday use.

25.1.0.1 Income

Income is what you earn from work plus what you receive in interest and dividends. It is a flow, meaning it is expressed per unit of time.

25.1.0.2 Saving

Saving is the part of after-tax income not spent, and it is also a flow. Savings is sometimes used as a synonym for wealth (a term we will not use here).

25.1.0.3 Financial wealth

Financial wealth, or simply wealth, is the value of all your financial assets minus liabilities. Unlike income or saving, financial wealth is a stock variable.

25.1.0.4 Investment

Investment is the purchase of new capital goods, like machines and buildings. Buying shares or financial assets is called financial investment.

25.1.0.5 Money

can be used for transactions but pays no interest.
two types of money:
- currency (coins and bills)
- checkable deposits (bank deposits on which you can write checks)

25.1.0.6 Bonds

Bonds pay a positive interest rate, $i$, but cannot be used for transactions.

Exercise 25.1 Don’t say “I have a lot of money”

Read the text below taken from Blanchard, 2013, p. 65. Understand the difference in meaning of money, income, and wealth:

In everyday conversation, we use money to denote many different things. We use it as a synonym for income: “making money.” We use it as a synonym for wealth: “She has a lot of money.”

In economics, you must be more careful. Here is a basic guide to terms and their precise meanings in economics.

Money is what can be readily used to pay for transactions. Money is currency and checkable deposits at banks.

Income is what you earn from working plus what you receive in interest and dividends. It is a flow—expressed in units of time: weekly, monthly, or yearly income, for example. J. Paul Getty was once asked his income. Getty answered: ” $1,000”. He meant $1,000 per minute!

Saving is part of after-tax income not spent. It is also a flow. If saving is 10% of income, and the income is $3,000 per month, then save $300 per month. Savings (plural) is sometimes used as a synonym for wealth. To avoid confusion, we will not use savings in this course.

Financial wealth, or simply wealth, is the value of all your financial assets minus financial liabilities. In contrast to income or saving, which are flow variables, financial wealth is a stock variable. It is wealth at a given moment in time.

At a given moment in time, you cannot change the amount of financial wealth. It changes over time as you save or dissave, or as the value of assets and liabilities change. But you can change the composition of wealth; for example, decide to pay back part of a mortgage by writing a check against a checking account. This reduces liabilities (smaller mortgage) and corresponding assets (smaller checking account balance); but does not change wealth at that moment.

Financial assets for buying goods are called money. Money includes currency and checkable deposits against which you can write checks. Money is also a stock. Someone wealthy might have small money holdings—$1,000,000 in stocks but $500 in a checking account. A person with large income might have small money holdings—$10,000 monthly but $1,000 in a checking account.

Investment is reserved for purchasing new capital goods. When talking about buying shares or financial assets, refer to them as financial investments.

Learn to be economically correct:

Do not say “I am making a lot of money”; say “I have a high income.”
Do not say “I have a lot of money”; say “I am very wealthy.”

25.2 The demand for money

Exercise 25.2 Money or bonds

How much will you hold of either? What determines your decision? What quantity of bonds would you hold if the interest rate was zero?

The demand for money comes from households, firms, and governments using money as a means of exchange and store of value. The law of demand holds: as the interest rate rises, the quantity of money demanded decreases because the interest rate represents an opportunity cost of holding money. Higher interest rates make money less effective as a store of value.

The demand for money depends on transactions in the economy and the interest rate. While transactions are hard to measure, they’re likely roughly proportional to nominal income. Demand for money is described as follows:

\[ M^d = \$Y \underbrace{L(i)}_{\frac{\partial L(i)}{\partial i} < 0} \]

Read this as: The demand for money $M^d$ equals nominal income $Y times a function of the interest rate $i$, denoted by $L(i)$. An increase in the interest rate decreases money demand as people shift more wealth to bonds.

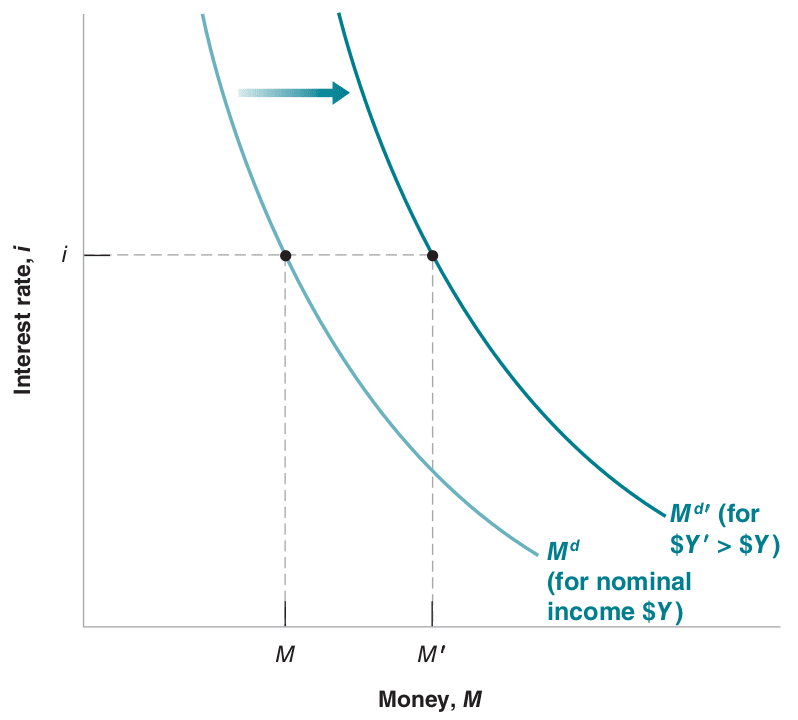
For a given nominal income, lower interest rates increase money demand. At a given interest rate, rising nominal income shifts money demand right. See Figure 25.1.

25.3 The supply of money and equilibrium

To find equilibrium in financial markets, understand that the price of money is the interest rate. Like any market, equilibrium is where demand and supply meet. Simplifying, assume monetary authorities (central banks) supply money and set interest rates.

A central bank can either choose money supply, setting interest rates where supply equals demand, or choose the interest rate and adjust money supply to achieve its chosen rate.

Equilibrium requires money supply equals money demand, $M = M^d$:

\[ \underbrace{M}_{\text{money supply}} = \underbrace{\$Y L(i)}_{\text{money demand}} \]

This equilibrium relation is called the LM relation where LM stands for Liquidity and Money.¹

Figure 25.2: The determination of the interest rate

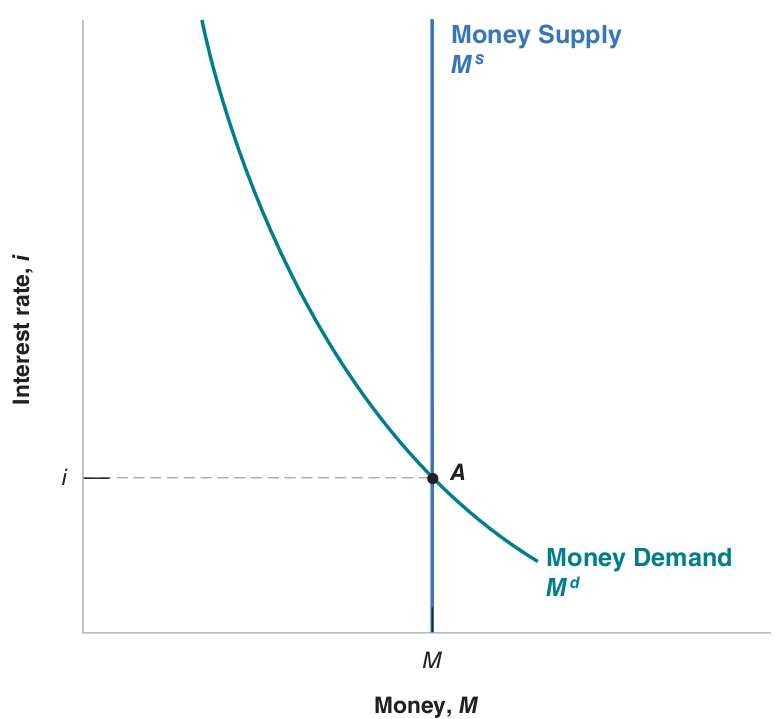
The interest rate must be such that money supply (independent of interest rate) equals money demand (dependent on interest rate). See Figure Figure 25.2.
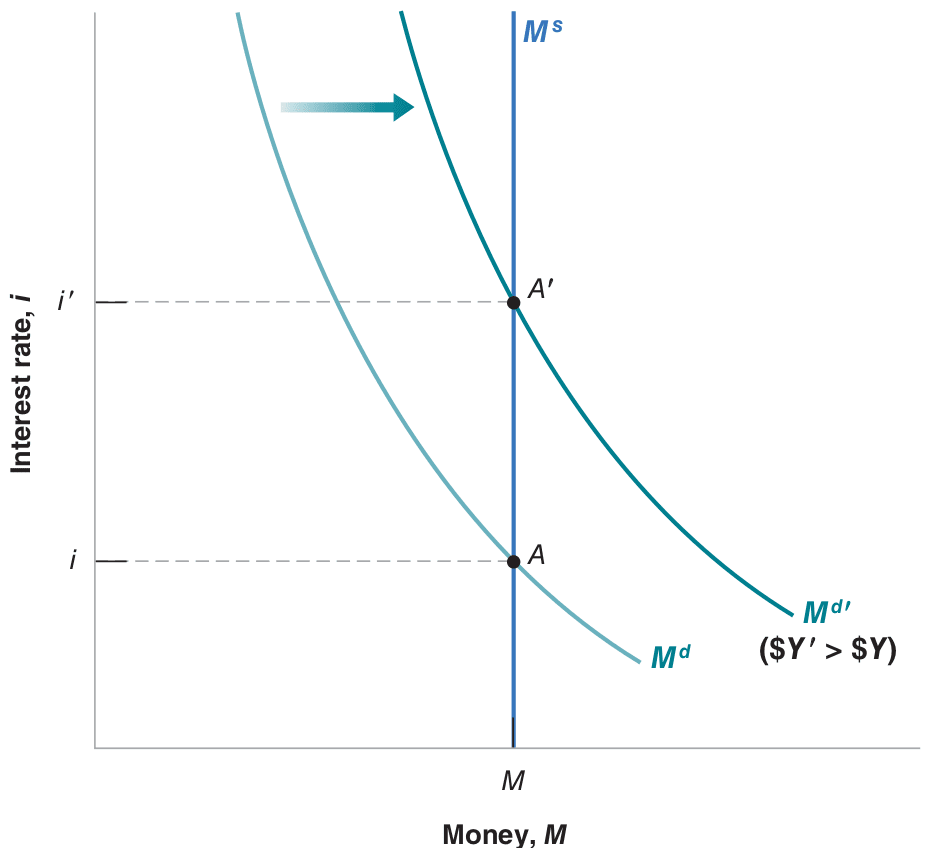
An increase in nominal income raises the interest rate as shown in Figure Figure 25.3.
- As mentioned, a central bank lowering interest rates from $i$ to $i'$ is akin to increasing money supply, seen in Figure Figure 25.5.

Figure 25.3: The effects of an increase in nominal income on the interest rate

Figure 25.4: The effects of an increase in the money supply on the interest rate

25.4 The derivation of the LM curve

25.4.1 Using algebra

Assuming money demand is linear:

\[ M^d = Y - hi \quad \text{with } h > 0 \]

The parameter $h$ represents how much demand for real money balances decreases as interest rates rise. Money supply ($M$) is set by the central bank and is assumed constant for a period. Solving for the interest rate gives the LM curve:

\[ i = \frac{1}{h} \left(Y - M\right) \]

25.4.2 Using graphs (see Figure 25.5)

Figure 25.5: Equilibrium in the goods market

An income increase, at a given interest rate, raises demand for money. Given supply, this demand rise increases the equilibrium interest rate.
Equilibrium in financial markets implies an income increase raises interest rates. The LM curve is upward sloping.

25.5 Taylor rule

The Taylor rule derives from empirical insights into how central banks operate.
It can replace the LM curve in the IS-LM Model, forming the IS-TR Model.
It’s a formula predicting central banks’ interest rate changes due to economic shifts.
The Taylor rule recommends raising interest rates when inflation or GDP growth exceed desired levels.
Critics say the Taylor principle can’t account for sudden economic shocks.
For more on the Taylor rule, see the Wikipedia entry: Taylor rule.
Formally, the rule is expressed as:

\[ i_{t} = \pi_{t} + r_{t}^{*} + a_{\pi}(\pi_{t} - \pi_{t}^{*}) + a_{y}(y_{t} - \bar{y}_{t}) \]

In this equation:

$i_t$: target short-term nominal interest rate,
$\pi_{t}$: inflation rate per GDP deflator,
$\pi _{t}^{*}$: desired inflation rate (target inflation rate),
$r_{t}^{*}$: assumed equilibrium real interest rate,
$y_{t}$: logarithm of real GDP,
$\bar{y}_{t}$: logarithm of potential output (linear trend).

Technical note on growth rates and logarithm

Taylor rule calculates $y_{t} - \bar{y}_{t}$. This linearly approximates growth rates—growth rate from time $t=0$ to $t=1$ in $x$ is approximately \[ \frac{x_1-x_0}{x_0} \approx \ln x_0 - \ln x_1 \]

Empirics showed it looks like this for central banks like the ECB and FED:

\[ i_{t} = \pi _{t} + 2 + 0.5(\pi _{t} - 2\%) + 0.5(y_{t} - {\bar y}_{t}) \]

Exercise 25.3 Taylor rule

Using the equation above, calculate the expected interest rate set by the central bank for the following inflation rates, $\pi_{t}$. Apply the Taylor Rule.

4%
1%
0%
-2% (Deflation)

Plot the Taylor Rule with $i$ on the y-axis and $Y$ on the x-axis.

Economists use liquidity as a measure of how easily an asset can be exchanged for money. Money is fully liquid; other assets less so.↩︎